Statistisk analyse for et mere sikkert emballagevalg

På Teknologisk Institut er en af de ypperste opgaver hos vores plast- og emballagespecialister at teste egenskaber af emballageløsninger for vores kunder. Til dette formål findes der tusindvis af forskellige standarder, der kan bruges til at beregne disse egenskaber, så det er muligt at sammenligne egenskaberne. Men hvad sker der hvis dette ikke er nok for kunden?

Denne artikel tager udgangspunkti en måling af barriereegenskaber vi blev bedt om at udføre for en kunde. Kunden havde en ny udformning på et låg de gerne ville have sammenlignet med deres nuværende låg. Til at beslutte sig om den nye udformning var værd at fortsætte med ville de derfor gerne kende barriereegenskaberne imod fugt. Til dette eksisterer standarden USP 671 (Metode 1), hvor 15 prøvemner bliver 2/3 fyldt med tørremiddel, bliver sat i et klimaskab i fem uger, hvorunder vægten noteres ugentligt. Vi modtog kort efter prøvemnerne af tre emballageløsninger og gik i gang med det samme.

Fem uger efter var testen færdig, baseret på disse foreskriver standarden at fugtens transmissionshastighed (MVT) bliver udregnet som hældningen af funktionen der beskriver vægt som funktion af tid for hver beholder. Derefter blev gennemsnit og standardafvigelsen for hver batch på 15 beregnet. Baseret på de opnåede værdier tegnede der sig en favorit.

Kunden ønskede dog mere belæg for deres beslutning, en bedre indsigt i sandsynlighedsfordelingen af barriereegenskaberne for at kunne vælge den bedste løsning.

Valg af statistisk hypotese

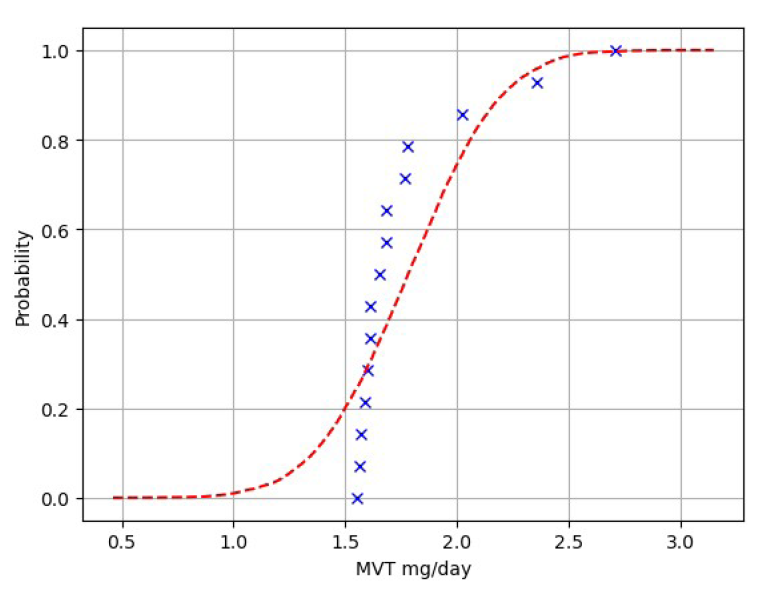
Standarden angiver gennemsnit og standardafvigelse som de to parametre der skal udregnes. Dette indikerede at barriereegenskaberne er normalfordelt. Da vi efterprøvede denne antagelse, fandt vi dog at dette ikke var tilfældet. Figur 1 viser denne efterprøvning, hvor den røde kurve angiver den teoretiske kumulative fordelingsfunktion for den Gaussiske normalfordeling, og de blå kryds angiver den observerede sandsynlighed. Ved sammenligning af disse to, kom vi frem til at en anden model måtte være gældende. Kunden havde derfor ret i, at mere dataanalyse kunne give et mere velfunderet beslutningsgrundlag.

Figur 1: Afprøvning af statistisk hypotese for emballageløsning 1. Blå kryds: den eksperimentelle kumulative fordelingsfunktion, rød kurve: normalfordeling simuleret ud fra gennemsnit og standardafvigelse af måleresultater.

Vi skulle dog stadig finde en retvisende statistisk model. Denne fandt vi efter at have afprøvet forskellige statiske modeller og hypoteser. Mere specifikt blev Gompertz-fordelingen identificeret som den mest retvisende model. Kort om denne model kan siges, at den typisk er brugt til systemer der oplever en mætning, fx beskriver den, at dødsraten for en population falder eksponentielt med populationens alder. Eksempelvis, medfører dette den åbenlyse konklusion at dødsraten er nul, hvis alle er døde.

Med denne model var det muligt at beskrive det observerede fænomen tilstrækkeligt for kunden. Ydermere kunne vi fra den kumulative fordelingsfunktion udregne sandsynlighedsfordelingen for barriereegenskaber, og vise denne grafisk (figur 2).

Figur 2: Sandsynlighedsfordelingen for barriereegenskaber for de tre testede emballageløsninger.

Hvad vi konkluderede

Ud fra statistisk analyse af måleresultaterne lærte vi ved brug af den kumulative fordelingsfunktion, at fordelingen af emballageløsningernes MVT’er passede på Gompertz-modellen. Vi konkluderede at emballageløsning 3 viste de bedste barriereegenskaber af de tre, dvs. laveste gennemsnitlige MVT og mindste spredning. Selvom det havde være muligt at tage et valg baseret på resultaterne fra standarden, viste modellering via Gompertz-fordelingen en mere retvisende fordeling af MVT end en normalfordeling.

Hvad kan vi hjælpe med

Hos Plast og Emballage har vi ud over at have styr på standarderne, også kompetencer i dataanalyse og formidling i resultaterne herfra. Dette betyder, at vi kan tilbyde vores kunder hjælp til avanceret statistisk analyse af resultaterne,
hvor det ønskes at kunne forudsige masseproducerede emballagers egenskaber.